Графический процессор в задачах обработки изображений
Проблема большого количества вычислений возникает в ряде задач многих направлений науки и техники. На сегодняшний день, когда с помощью компьютеров решаются, чуть ли не все задачи человечества, применение электронных вычислительных машин является естественно разумным шагом. Среди всего множества задач можно выделить некоторый спектр, для решения которых требуется от нескольких часов до нескольких дней машинного времени. Среди таких ресурсоемких в вычислительном плане задач и направлений можно отметить следующие: предсказание погоды, климата и глобальных изменений в атмосфере, генетика человека, астрономия, транспортные задачи, гидро- и газодинамика, управляемый термоядерный синтез, разведка нефти и газа, вычислительные задачи наук о мировом океане, распознавание изображений и синтез речи. Использование суперкомпьютеров с большим количеством независимо работающих параллельных процессоров и технологий высокопроизводительных вычислений может существенно снизить заявленные выше временные оценки. Такой подход
является заведомо очень дорогим в финансовом плане и позволителен для узкого круга исследователей и ученых. Тем не менее, сейчас в области настольных персональных компьютеров начинают широко распространяться процессоры с несколькими независимыми ядрами, что позволяет решать уже некоторые задачи в параллельном режиме более широкому кругу обычных пользователей и специалистов. Однако количество ядер в таких процессорах ограничено, как правило, двумя либо четырьмя штуками, что не всегда дает особого приращения производительности. Но современный персональный компьютер в большинстве случаев может быть оснащен сегодня помимо мощного центрального процессора (CPU - Central Processing Unit) еще и современной видеокартой с графическим процессором (GPU - Graphics Processing Unit) производительностью несколько сотен миллиардов операций с плавающей точкой в секунду. Даже самые современные серверные процессоры далеки от такой производительности. Вообще изначально область применения графического пр оцессора была просчет и отображение трехмерных сцен.
Однако, с появлением видеокарт, позволяющих их программировать, круг вычислительных задач, решаемых с помощью графического процессора, существенно расширился. Поэтому возникает резонный вопрос. Почему бы не задействовать вычислительные ресурсы графического процессора для решения задач отличных от его "традиционных" графических? Как мы уже уяснили, обработка вершин и пикселей в графическом конвейере ведется в параллельном режиме. Количество параллельных блоков по преобразованию вершин зависит от модели графического процессора и может колебаться от 2 до 8 штук. Аналогично блок пиксельной обработки также функционирует в параллельном режиме, причем количество пиксельных блоков может быть от 4 до 48 штук в зависимости от типа видеокарты (на момент написания данных строк).
В качестве области исследования и проведения вычислительных экспериментов рассмотрим точечные процессы цифровой обработки изображений. С цифровой обработкой изображений сталкиваются при решении многих научных и технических задач. Обработка изображений в широком смысле слова означает выполнение различных операций над многомерными сигналами, которыми изображения и являются. Цели, преследуемые при обработке изображений весьма различны и, как правило, зависят от конкретной решаемой задачи. Это может быть улучшение яркости или контраста в вашей домашней коллекции цифровых фотографий, получение монохромных (бинарных) изображений, обработка изображений сглаживающими фильтрами для удаления шумов и мелких искажений, выделение значимых признаков на изображении с применением в последствии алгоритмов распознавания, например, формы символов. Современная жизнь ставит ряд требований к подобным методам обработки. Одно из самых главных это высокая эффективность и скорость работы алгоритмов с использованием персонального
ФЄ компьютера. Традиционно обработкой изображений занимался центральный процессор системы. Для этого каждый элемент изображения (пиксель) подвергался некоторому, как правило, однотипному преобразованию.
И в результате получалось, что для изображения размерами M на N пикселей требуется MxN операций процессора. При значительных размерах изображения этот объем вычислений может оказаться критическим для одного устройства обработки информации. Поэтому, чтобы снизить вычислительную нагрузку алгоритма вполне резонно воспользоваться идеями и методами параллельных вычислений. Однако привлечение дорогостоящих параллельных суперкомпьютеров в данной задаче не является критически необходимым. Подобный класс задач можно попытаться решить с помощью обычной современной видеокарты, стоимость которой на несколько порядков меньше любого вычислительного кластера. Под точечными процессами будем понимать набор алгоритмов, которые подвергают обработке каждый пиксель изображения независимо от оста льных элементов. Примерами точечных пр оцессов могут выступать: приведение цветного изображения к оттенкам серого цвета, увеличение/уменьшение яркости и контраста, негативное преобразование, пороговое отсечение, соляризация и др. Следует отметить, что перечисленные точечные процессы мы будем рассматривать для изображений в оттенках серого цвета, так называемых grayscale. В подобных изображениях присутствуют только 256 оттенков какого-либо основного цвета. Как правило, используются оттенки серого цвета так, что палитра цветов содержит 256 "плавноизменяющихся" от черного к белому цвету интенсивностей. При этом черный цвет кодируется нулем, белый – числом 255. Таким образом, точечный процесс можно представить как некую функцию, определенную на целочисленном дискретном множестве [0…255] с таким же множеством значений.
Преобразование просветления увеличивает или уменьшает значение яркости каждого пикселя в отдельности. Пусть I(x,y) – значение яркости пикселя (x,y) в изображении I. Тогда операция просветления на языке формул может быть выражена следующим образом: I(x,y)= I(x,y)+b, где b – постоянная яркости. Если b>0, то яркость в изображении будет увеличиваться (просветление); если же b<0, то яркость будет уменьшаться (затемнение).
Могут возникнуть случаи, при которых значение выражения I(x,y)+b выйдет за пределы отрезка [0…255]. В этом случае значение, вышедшее за границы отрезка приводят к значению ближайшей границы, т.е. либо к 0, либо к 255. Графически операцию просветления можно описать следующими графиками функций.
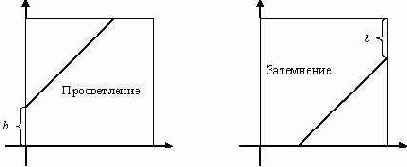
Рассмотрим произвольное изображение I в оттенках серого цвета. Введем массив H, содержащий 256 элементов: H[0…255]. Каждый i-й элемент этого массива будет содержать количество пикселей в изображении I со значением интенсивности i. Если визуализировать массив H в виде графика функции, то получим так называемую гистограмму интенсивностей яркости исходного изображения I. Вид гистограммы позволяет получить представление об общей яркости изображения. Гистограмма интенсивности является информативным инструментом при анализе общей яркости в изображении. Способ получения гистограммы интенсивности изображения можно записать на алгоритмическом языке следующим образом.
Цикл по x от 0 до ШиринаИзображения-1 Цикл по y от 0 до ВысотаИзображения-1 ТелоЦикла k = I(x,y); H[k] = H[k] + 1; КонецТелоЦикла
Ниже на рисунке приведены три гистограммы интенсивности различного класса.
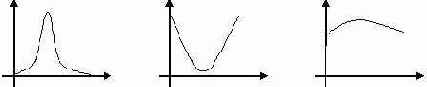
Гистограмма слева определяет изображения, в которых мало пикселей черного и белого цветов (низкоконтрастные изображения). Гистограмма посередине соответствует изображениям, в которых число черных и белых пикселей значительно превышает все остальные (высококонтрастные изображения). И гистограмма справа представляет изображения, в которых количество пикселей с различными интенсивностями цветов приблизительно одинаково (нормальноконтрастные изображения). Изменение контраста в изображении можно осуществить с помощью линейных преобразований. Для гистограмм, соответствующих низкоконтрастным изображениям, выделяют отрезок [Q1,Q2], на котором сосредоточена значительная часть интенсивностей. Затем данный отрезок [Q1,Q2] линейно отражают в отрезок [0…255] с помощью следующего преобразования: I(x,y)= 255*(I(x,y)-Q1)/(Q2-Q1). Аналогично можно получить формулу для уменьшения контраста в изображении.
В этом случае преобразование будет иметь следующий вид: I(x,y)= R1+I(x,y)*(R2-R1)/255, где [R1,R2] – некий отрезок, в который отображается все множество значений интенсивностей. Графически операции увеличения и уменьшения контрастности в изображении можно представить следующим образом.
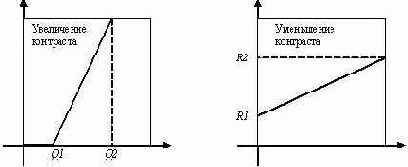
Негативное преобразование инвертирует значения интенсивностей яркости так, что темные пиксели становятся светлыми и наоборот. Математически это задается довольно простой формулой:
I(x,y)= 255- I(x,y), а графически это выглядит следующим образом.
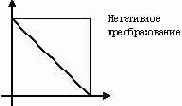
Пороговое отсечение (бинаризация) преобразует изображение в оттенках серого в изображение, в котором присутствует всего два цвета, как правило, белый и черный (бинарное). На языке формул бинаризация имеет такой вид: I(x,y)=0, если I(x,y)>p; I(x,y)=255, если I(x,y)<p, где p – некоторый заданный порог. Графически операция порогового отсечения задается следующим образом.
Очень часто пороговое отсечение применяется как промежуточный шаг в задачах распознавания изображений для устранения ошибок сканирования и оцифровки.
Получение изображения в оттенках серого из цветного также можно отнести к точечным процессам. Каждый пиксель цветного изображения представляет собой тройку байт, значения которых соответствуют весам красного, зеленого и синего цветов. Это так называемая цветовая модель RGB (Red, Green, Blue). Преобразование цветного изображения в оттенки серого осуществляется по следующей формуле:
I=0.3*R+0.59*G+0.11*B, где I – значение интенсивности серого цвета, R, G, B - значения весов красного, зеленого и синего цветов соответственно.
Ниже представлены результаты обработки исходного изображения пиксельным шейдером.
sampler tex0;
struct PS_INPUT { float2 base : TEXCOORD0; }; struct PS_OUTPUT { float4 diffuse : COLOR0; }; PS_OUTPUT Main (PS_INPUT input) { PS_OUTPUT output; float4 col = tex2D(tex0, input.base); ... return output; };
| Исходное изображение |  |
| Приведение к оттенкам серого цвета float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); output.diffuse = dot(lum,col); |  |
| Увеличение яркости float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); output.diffuse = dot(lum,col)+0.2f; |  |
| Уменьшение яркости float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); output.diffuse = dot(lum,col)-0.2f; |  |
| Увеличение контраста float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); float Q1 = 0.2f; float Q2 = 0.7f; if (gray > Q2) gray = 1.0f; else if (gray < Q1) gray = 0.0f; else gray = (gray - Q1)/(Q2-Q1); output.diffuse = gray; |  |
| Уменьшение контраста float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); float R1 = 0.2f; float R2 = 0.7f; gray = R1+gray*(R2-R1); output.diffuse = gray; |  |
| Пороговое отсечение (бинаризация) float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); float p = 0.4f; if (gray > p) gray = 1.0f; else if (gray < p) gray = 0.0f; output.diffuse = gray; |  |
| Негативное преобразование float4 col = tex2D(tex0, input.base); float4 lum = float4(0.3, 0.59, 0.11, 0); float gray = dot(lum,col); output.diffuse = 1.0f-gray; |  |
Рассмотрим теперь некоторые методы обработки изображения с использованием пространственных процессов. В этом случае элемент изображения получает новое значение на основе группы элементов, примыкающих к данному. Область (окрестность) примыкания представляет собой группу элементов изображения использующаяся в пространственных процессах. Как правило, область примыкания есть квадратная матрица нечетной размерности с центром в обрабатываемом элементе.
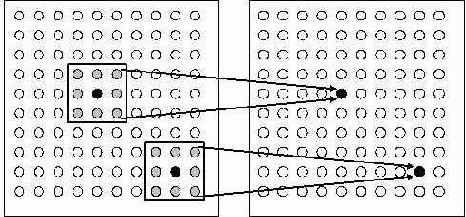
Пространственная частота изображения – скорость изменения яркости по координатам. Говорят, что присутствует высокая частота в изображении, если яркость меняется очень сильно. Одной из центральных задач в обработке изображений является построение пространственного фильтра. Фильтр позволяет усилить или ослабить компоненты различной частоты. Пространственный фильтр – процесс, который способен выделить (подчеркнуть) компоненты определенной частоты. Двумерный фильтр устроен следующим образом. Берется матрица размером 3х3, 5х5, 7х7 и т.д. и на ней определяется некоторая функция Упомянутая матрица называется окном или апертурой, а заданная на нем функция – весовой или функцией окна. Каждому элементу окна соответствует число, называемое весовым множителем. Совокупность всех весовых множителей и составляет весовую функцию. Нечетные размеры апертуры объясняются однозначностью определения центрального элемента. Фильтрация осуществляется перемещением окна (апертуры) фильтра по изображению. В каждом положении апертур
ФЄ ы выполняются однотипные действия, которые определяют так называемый отклик фильтра. Весовая функция в процессе перемещения остается неизменной. В каждом положении окна происходит операция свертки – линейная комбинация значений элементов изображения:




Низкочастотный фильтр – процесс, который ослабляет высокочастотные компоненты и усиливает роль низкочастотных.
Сглаживание изображения реализуется с помощью следующих ядер.

Следует заметить, что общая яркость исходного изображения и результирующего будет одинаковой.
Фильтры высокой частоты применяются для выделения таких деталей, как контуры, границы или для повышения резкости изображения. Каждый скачок яркости и каждый контур представляют собой интенсивные детали, связанные с повышенными частотами. С помощью высокочастотного фильтра можно так видоизменить изображение, чтобы скачки яркости на контурах будут сильно подчеркнуты, а в предельном случае вообще останутся только контуры. Ниже приведены примеры ядер высокочастотных фильтров.

Медианный фильтр – пространственный процесс, который не подпадает под категорию свертки. Усредненное фильтрование использует значения элементов, содержащихся в области примыкания, для определения нового значения. Фильтр располагает элементы области примыкания в возрастающем порядке и отбирает среднее значение.

Результатом усредненного фильтра является то, что любой случайный шум, содержащийся в изображении, будет устранен. Это происходит потому, что любое случайное резкое изменение интенсивности элемента в пределах области примыкания, будет сортироваться, т.е. будет помещено либо в начало, либо в конец отсортированного списка.
Другим пространственным процессом, который можно продемонстрировать, используя свертку, является усиление края. В отличие от задачи обострения контуров (высокочастотный фильтр) здесь основной целью является не улучшение изображения, а наоборот, контуры должны быть отделены от всего изображения так, чтобы выходное изображение состояло только из контуров. Рассмотрим основные методы усиления края.
Метод усиления края по Лапласу не зависит от направления краев, и высвечиваются все направления. Ниже приведены три лапласиана.

Метод усиления края с помощью оператора Собеля рассматривает два различных ядра свертки:

Исходя из этих сверток, вычисляется величина и направление краев.
В качестве отклика данного фильтра выступает величина



Метод усиления края с помощью оператора Превита также использует два ядра:

Результат работы оператора Превита есть max{P,Q}, где P и Q - отклики ядер


Метод преобразования реализующий эффект тиснения на изображении. Результирующее изображение выглядит как будто "выдавленным" или "вдавленным". Фильтр такого преобразования имеет вид:

Как нам известно, обращение к элементам текстуры в пиксельном шейдере производится с помощью текстурных координат. Левый верхний тексель имеет текстурные координаты (0,0), левый нижний – координаты (0,1), правый верхний – координаты (1,0), правый нижний – координаты (1,1)

Задача состоит в том, чтобы для произвольного текселя изображения, имеющего текстурные координаты (u,v), определить значения текстурных координат восьми его соседей. Пусть у нас количество текселей в каждой строке будет W, а количество текселей в каждом столбце – H. В силу того, что тексели расположены равномерно (на одинаковом расстоянии друг от друга), можно вычислить шаг приращения du и dv в текстурных координатах по горизонтали и вертикали соответственно. Итак,



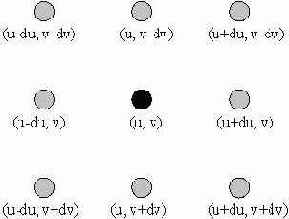
Ниже приведен пример пиксельного шейдера, который реализует метод усиления границ на изображении с помощью оператора Собеля и метод тиснения, а также примеры изображений.
sampler tex0;
struct PS_INPUT { float2 base : TEXCOORD0; };
struct PS_OUTPUT { float4 diffuse : COLOR0; };
PS_OUTPUT Main (PS_INPUT input) { PS_OUTPUT output; const float W =320.0f; const float H =240.0f; const float du=1.0f/(W-1); const float dv=1.0f/(H-1); const float2 c[9] = { float2(-du, -dv), float2(0.0f, -dv), float2(du, -dv), float2(-du, 0.0f), float2(0.0f, 0.0f), float2(du, 0.0f), float2(-du, dv), float2(0.0f, dv), float2(du, dv) };
float3 col[9]; for (int i=0; i<9; i++) { col[i] = tex2D(tex0, input.base+c[i]); }
float lum[9]; float3 gray = (0.30f, 0.59f, 0.11f) ; for (int i=0; i<9; i++) { lum[i] = dot(col[i], gray); }
float res1 = 0.0f; float res2 = 0.0f; const float sobel1[9] = { 1, 2, 1, 0, 0, 0, -1, -2, -1}; const float sobel2[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1}; const float tisnenie[9] = {0, 1, 0, -1, 0, 1, 0, -1, 0}; for (int i=0; i<9; i++) { res1+=lum[i]*sobel1[i]; res2+=lum[i]*sobel2[i]; res+=lum[i]*tisnenie[i]; } output.diffuse = sqrt(res1*res1+res2*res2); //output.diffuse = res+0.5f; return output; };
Пример 6.1.
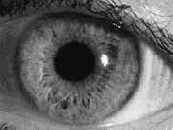
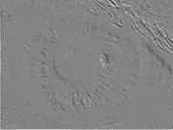
| Исходное изображение | Оператор Собеля | Метод тиснения |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
