Реалистичные построения
Принцип текстурирования трехмерных объектов ничем не отличается от двумерного аналога. Для каждой треугольной грани необходимо задать текстурные координаты. Единственное отличие от двумерного варианта заключается в формате вершин и наборе FVF флагов.
| C++ |
struct VERTEX3D { FLOAT x, y, z; FLOAT u, v; }; #define MY_FVF (D3DFVF_XYZ | D3DFVF_TEX1); ... VERTEX3D points[3] = { { -1.0f,-1.0f, 0.0f, 0.0f, 1.0f, }, { 0.0f, 1.0f, 0.0f, 0.5f, 0.0f, }, { 1.0f,-1.0f, 0.0f, 1.0f, 1.0f, } } |
| Pascal |
type Vertex3D = packed record x, y, z: Single; u, v: Single; end; const MY_FVF = D3DFVF_XYZ or D3DFVF_TEX1; var points: array [0..2] of Vertex3D = ( (x: -1; y: -1; z: 0; u: 0; v: 1), (x: 0; y: 1; z: 0; u: 0.5; v: 0), (x: 1; y: -1; z: 0; u: 1; v: 1) ); |
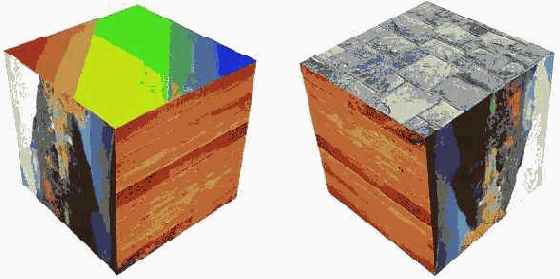
Ниже показан пример вывода куба, у которого все грани покрыты различными текстурами. Для этого можно объявить массив для хранения текстур из шести элементов типа IDirect3DTexture9.
| C++ |
LPDIRECT3DTEXTURE9 textures[6]; LPCSTR files[] = { {"bricks.bmp"}, {"colors.bmp"}, {"Lake.bmp"}, {"stone_wall.bmp"}, {"wall.bmp"}, {"fur.jpg"} }; ... for (int i=0; i<6; i++) D3DXCreateTextureFromFile( device, files[i], &textures[i] ); |
| Pascal |
var textures: array [0..5] of IDirect3DTexture9; files: array [0..5] of AnsiString = ( ('bricks.bmp'), ('colors.bmp'), ('Lake.bmp'), ('stone_wall.bmp'), ('wall.bmp'), ('fur.jpg') ); ... for i:=0 to 5 do D3DXCreateTextureFromFile(device, PChar(files[i]), textures[i]); |
Теперь если куб у нас храниться в виде 12 независимых треугольных граней, то его вывод может быть осуществлен с помощью следующего кода.
| C++ |
for (int i=0; i<6; i++) { device->SetTexture(0, &textures[i]); device->DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); } |
| Pascal |
for i:=0 to 5 do begin device.SetTexture(0, textures[i]); device.DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); end; |
Ниже приведены примеры (кадры анимации) вращения такого куба.
Рассмотрим один из способов построения полупрозрачных трехмерных объектов.
Данный метод прозрачности применим только для выпуклых объектов. Идея его заключается в следующем. Вначале выводятся те грани объекта, которые считаются невидимыми для наблюдателя (задние грани). Затем включается режим полупрозрачности (смешивания цветов). Выводим грани объекта, которые видны наблюдателю. Отображение "передних" и "задних" для наблюдателя сторон объекта можно осуществить с помощью механизма отсечения граней. Предположим, что вершины грани перечислены по часовой стрелке. Тогда отключение вывода таких граней отобразит нам "задние" стороны примитива (в нашем случае куба). Программно этот шаг может выглядеть так.
| C++ | device->SetRenderState( D3DRS_CULLMODE, D3DCULL_CW ); for (int i=0; i<6; i++) { device->SetTexture(0, &textures[i]); device->DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); } |
| Pascal | device.SetRenderState(D3DRS_CULLMODE, D3DCULL_CW); for i:=0 to 5 do begin device.SetTexture(0,textures[i]); device.DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); end; |

Включение полупрозрачности с нужными параметрами смешивания цветов.
| C++ | device->SetRenderState( D3DRS_ALPHABLENDENABLE, TRUE ); device->SetRenderState( D3DRS_SRCBLEND, D3DBLEND_SRCCOLOR ); device->SetRenderState( D3DRS_DESTBLEND, D3DBLEND_INVSRCCOLOR ); |
| Pascal | device.SetRenderState(D3DRS_ALPHABLENDENABLE, 1); device.SetRenderState(D3DRS_SRCBLEND, D3DBLEND_SRCCOLOR); device.SetRenderState(D3DRS_DESTBLEND, D3DBLEND_INVSRCCOLOR); |
| C++ | device->SetRenderState( D3DRS_CULLMODE, D3DCULL_CCW ); for (int i=0; i<6; i++) { device->SetTexture(0, &textures[i]); device->DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); } |
| Pascal | device.SetRenderState(D3DRS_CULLMODE, D3DCULL_CCW); for i:=0 to 5 do begin device.SetTexture(0,textures[i]); device.DrawPrimitive(D3DPT_TRIANGLELIST, i*6, 2); end; |
Для придания трехмерной сцене еще большей реалистичности можно добавить тени, которые отбрасывают объекты при освещении их некоторым источником света. Алгоритмы затенения в случае точечных источников света схожи с алгоритмами удаления невидимых поверхностей, с единственным лишь отличием. В алгоритмах удаления невидимых граней определяются поверхности, которые можно увидеть из точки положения наблюдателя, а в алгоритмах затенения выделяются поверхности, которые можно "увидеть" из местоположения источника света. Грани, видимые как из точки наблюдения, так и из источника света, не лежат в тени. Те же поверхности, которые видимы из точки наблюдения, но не видимы из источника света, находятся в тени.
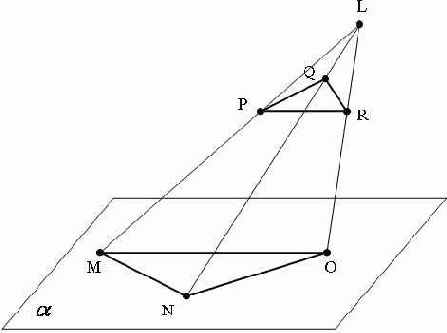
Рассмотрим один из простейших и очень быстрых алгоритмов построения теней. Он предназначен для просчета резких теневых участков от полигональных объектов на ровную поверхность (плоскость). Конечно, этот алгоритм очень ограничен в возможностях, но в то же время он прост для реализации. Основная идея метода заключается в том, что для каждого полигона (треугольной грани) сцены, создается еще один полигон, который будет представлять собой тень первого. Все вершины тени будут находиться в пределах плоскости, на которую производится проекция. Алгоритм построения тени будет содержать следующие шаги:
- Создать луч, начинающийся в источнике света, проходящий через вершину полигона и пересекающий плоскость проецирования;
- Получить (найти) точку пересечения этого луча с плоскостью;
- Проделать шаги 1 и 2 для всех вершин грани, получив таким образом координаты "теневого" полигона и затем отрисовать его обычными методами.
Пусть у нас источник света находится в точке L=(Lx,Ly,Lz), треугольная грань объекта имеет координаты вершин P=(Px,Py,Pz), Q=(Qx,Qy,Qz), R=(Rx,Ry,Rz), а плоскость проецирования (затенения)




С другой стороны точка M лежит в плоскости

Подставим выражения для Mx,My,Mz в уравнение плоскости: A*(Lx+t(Px-Lx))+B*(Ly+t(Py-Ly))+C*(Lz+t(Pz-Lz))+D=0. Это линейное уравнение относительно параметра t, решая которое находим, что



Аналогичные шаги проделываем для двух других вершин полигона Q и R. Следует заметить, что при вычислении тени на плоскость y=0, параметр

Рассмотренный метод имеет несколько "подводных камней". Тень будет прорисовываться даже в том случае, если источник света находится между полигоном и плоскостью проецирования или же источник света расположен вообще по другую сторону от плоскости. Поэтому такие ситуации необходимо отслеживать и корректно обрабатывать.
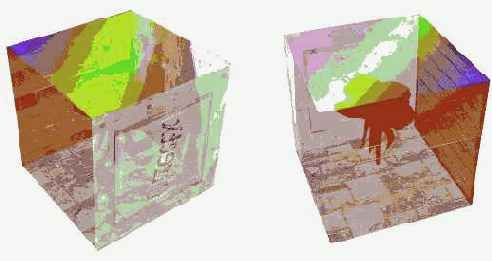
Ниже приводится пример отбрасывания тени от трехмерного объекта (птицы) на плоскость, покрытую текстурой. В одном случае "тень" является непрозрачной, а в другом – прозрачной.

Рассмотрим способ построения ландшафтов и поверхностей средствами библиотеки Direct3D. Данная задача сводится к тому, чтобы на регулярной сетке из треугольников построить трехмерную поверхность (график функции двух переменных, земная поверхность, и т.п.).
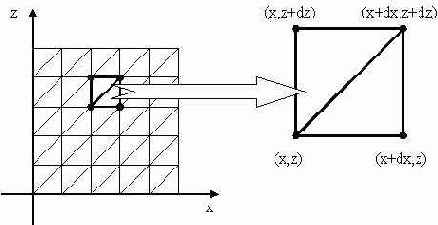
Разберем построение трехмерной поверхности, представляющей собой функцию двух переменных y=f(x,z). Пусть для простоты у нас область определения функции f(x,z) ограничена единичным квадратом, т.е. 0<=x<=1, 0<=z<=1. Визуализация рассмотренных поверхностей на растровых устройствах может быть осуществлена путем кусочно-линейной аппроксимации треугольными гранями. Такая триангуляционная поверхность может быть получена следующим образом. Параметрическое пространство x,z (единичный квадрат) дискретизируется по координате x с шагом dx, по координате z – с шагом dz. Для каждой пары значений (x,z) вычисляется точка на поверхности y=f(x,z). Полученный таким образом массив точек триангулируется регулярной сеткой.
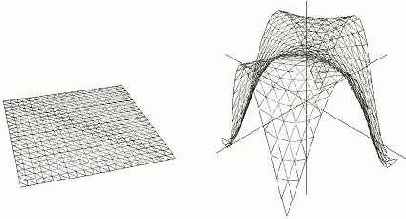
Ниже приведены два примера построения трехмерных поверхностей (график функции двух переменных и элементарная поверхность Безье третьей степени) , причем на обе поверхности наложены текстуры.


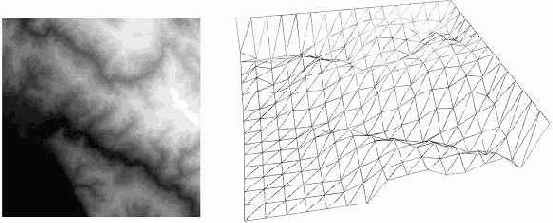
Разберем один из способов построения ландшафтов, который базируется на так называемой карте высот. Карта высот представляет собой двумерный массив, где каждый элемент (пиксель) определяет высоту точки в сетке треугольников. Как правило, значение высоты ранжируется в диапазоне от 0 до 255. Поэтому для хранения подобных карт высот используют изображения в оттенках серого цвета (grayscale image). Более светлые участки на таких изображениях соответствуют более высоким значениям точек, а темные участки определяют низкие значения высот. Кроме этого подбирается текстура, схожая по "характеру" с ландшафтом. Ниже приведен пример построения ландшафта по карте высот.